Mastering PCA and k-means Clustering: A Comprehensive Guide for Data Scientists
PCA simplifies datasets by reducing dimensionality, preserving variance. Data standardization ensures equal feature contribution, crucial for algorithms like PCA and clustering. Optimal cluster number can be determined using metrics like Elbow Method, Silhouette Score, and Calinski-Harabasz Index for meaningful data segmentation.
Mastering PCA and k-means Clustering: A Comprehensive Guide for Data Scientists
Description:
Hello everyone! 🌟 In this video, we dive deep into the fascinating world of machine learning, focusing on Principal Component Analysis (PCA) and its application in clustering algorithms like k-means. We’ll cover:
- The theoretical foundations of PCA
- The importance of data standardization
- How to determine the optimal number of clusters using various metrics
By the end of this video, you’ll have a solid understanding of how to effectively use PCA and k-means clustering to enhance your data science projects. Don’t forget to like, comment, and subscribe for more insightful content!
Links to the Implementations Used
Here are the links to the scikit-learn documentation for the different implementations mentioned in this article:
- Calinski-Harabasz Index: sklearn.metrics.calinski_harabasz_score
- Elbow Method: The Elbow Method is not a direct function in scikit-learn, but it is implemented using the KMeans model’s inertia attribute. See the KMeans documentation for more details: sklearn.cluster.KMeans
- K-Means Clustering: sklearn.cluster.KMeans
- PCA (Principal Component Analysis): sklearn.decomposition.PCA
- Standard Scaler: sklearn.preprocessing.StandardScaler
- Silhouette Score: sklearn.metrics.silhouette_score
Theoretical Foundations of PCA
Principal Component Analysis (PCA) is a statistical technique used to simplify complex datasets by reducing their dimensionality while preserving as much variance as possible. PCA transforms the original variables into a new set of uncorrelated variables, known as principal components, ordered by the amount of variance they capture from the data. This method helps in visualizing high-dimensional data and identifying patterns, making it easier to perform further analysis.
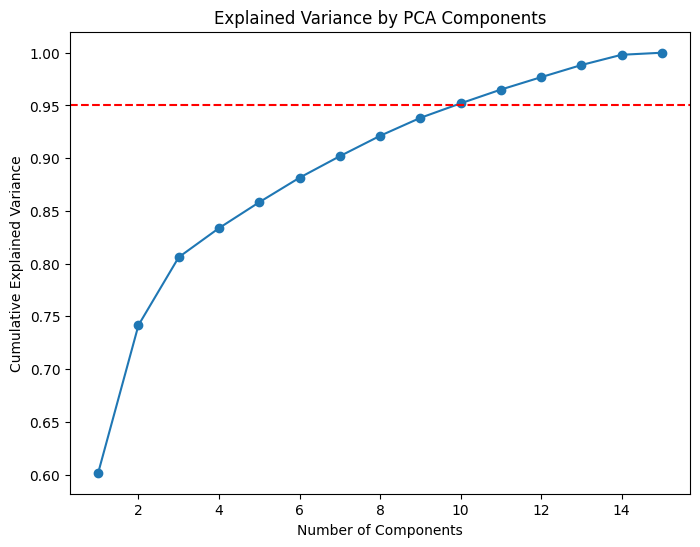
The Importance of Data Standardization
Data standardization is a crucial preprocessing step in machine learning and data analysis. It involves transforming the data to have a mean of zero and a standard deviation of one. This process ensures that all features contribute equally to the analysis, preventing features with larger scales from dominating the results. Standardization is particularly important for algorithms like PCA and clustering, which are sensitive to the scales of the input data.
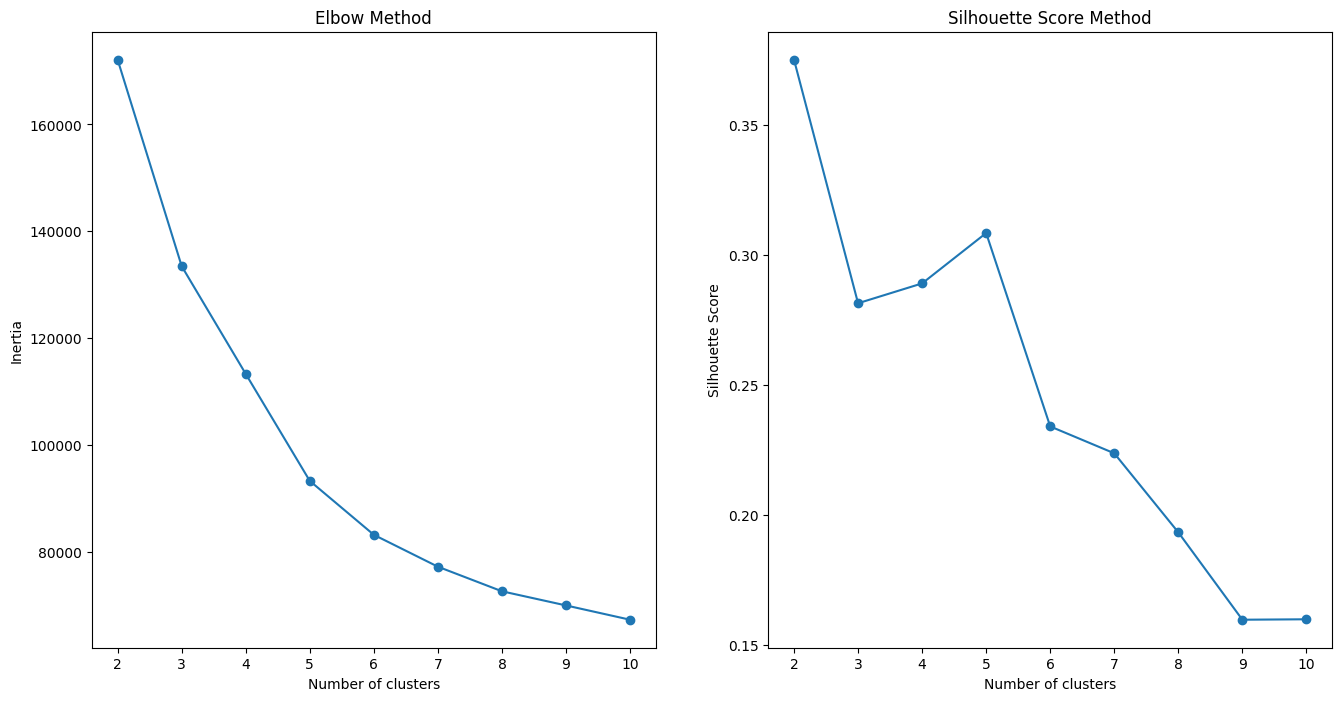
Determining the Optimal Number of Clusters Using Various Metrics
Choosing the optimal number of clusters in clustering algorithms like K-means is essential for meaningful data segmentation. Several metrics can help determine this number, including the Elbow Method, Silhouette Score, and Calinski-Harabasz Index. The Elbow Method involves plotting the within-cluster sum of squares against the number of clusters and looking for an “elbow” point. The Silhouette Score measures how similar an object is to its own cluster compared to other clusters, with higher scores indicating better-defined clusters. The Calinski-Harabasz Index evaluates the ratio of the sum of between-cluster dispersion and within-cluster dispersion, with higher scores indicating better-defined clusters. Using these metrics helps in finding a balance between simplicity and accuracy in the clustering results.
The Podcast
Tags:
#DataScience, #MachineLearning, #PCA, #PrincipalComponentAnalysis, #KMeans, #Clustering, #DataStandardization, #SilhouetteScore, #CalinskiHarabaszScore, #ElbowMethod, #Python, #Sklearn, #DataAnalysis, #DimensionalityReduction, #Eigenvalues, #Eigenvectors, #MLAlgorithms, #DataPreprocessing, #DataVisualization, #TechTutorials, #AI, #ArtificialIntelligence