Statistical Interpretation of Tabular Data, Part 4

Advanced statistical visualization techniques for data interpretation, including dendrograms, Spearman rank correlation, and partial dependence plots.

Tags: statistical-data-interpretation advanced-visualizations dendrogram correlation-analysis tabular-data

Category: Tabular Data

Series: Kaggle Competition Deep Dive Tabular Data

Advanced Missing Value Analysis in Tabular Data, Part 1
Decision Tree Feature Selection Methodology, Part 2
RandomForestRegressor Performance Analysis, Part 3
Statistical Interpretation of Tabular Data, Part 4
Addressing the Out-of-Domain Problem in Feature Selection, Part 5
Kaggle Challenge Strategy: RandomForestRegressor and Deep Learning, Part 6
Hyperparameter Optimization in Deep Learning for Kaggle, Part 7

Statistical Interpretation of Tabular Data, Part 4

Dendrogram Visualization For Spearman Rank Correlations

With the scipy library, one can create a Dendrogram using the features in the training set. Using the Spearman rank correlation (\(\rho\)), which does not have any prerequisites in terms of the relationships between the features, e.g., a linear relationship, the rank correlation is used to calculate the correlations. The final plot applies the same color to features whose rank correlation values are close to each other. On the x-axis, one can see the strength of the correlation, with close to zero indicating that the assumed linear relationship between the features in this group is one of no consistent change. Values close to one indicate a close to perfect monotonic relationship. \(H_0\) is that each variable pair is uncorrelated.

def cluster_columns(df, figsize=(12, 12), font_size=10):
    i = 'average'
    corr = scipy.stats.spearmanr(df).correlation
    z = hc.linkage(corr, method=i)
    fig = plt.figure(figsize=figsize)
    hc.dendrogram(z, labels=df.columns,
                  orientation="left",distance_sort=True, leaf_font_size=font_size)
    plt.title(f'Dendrogram Of Correlation Clusters\nMethod: "{i}"')
    plt.ylabel('Feature Names By Cluster')
    plt.xlabel(r"Cluster Hierarchy Using Spearman $\rho$")
    plt.show()

cluster_columns(xs_imp)

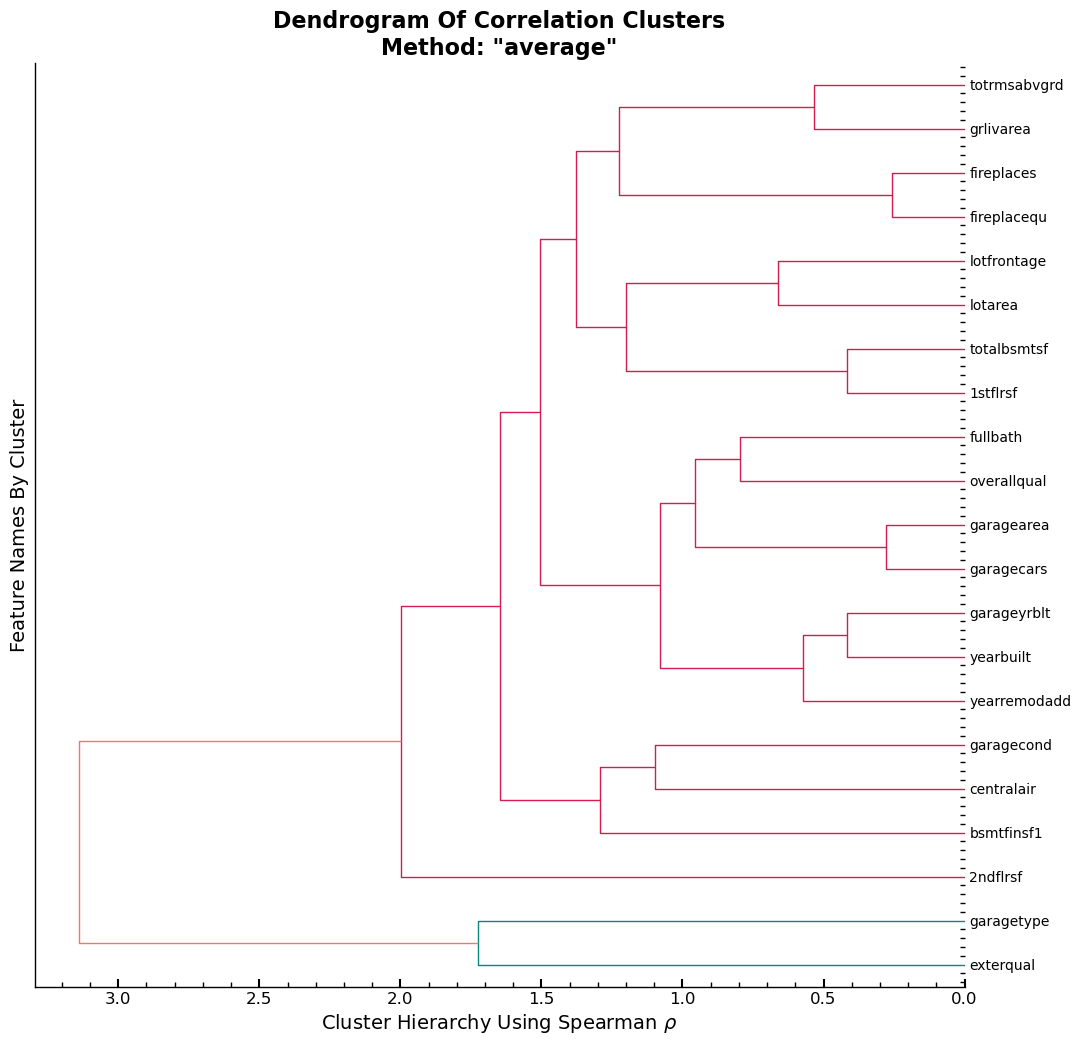
Conclusion

The output shows that variable garagetype and exterqual are assumed to have a high similarity and are the two columns with the strongest assumed linear relationship among the features found in xs_imp.

Dendrogram Findings Applied

To test what the impact of dropping even more features from xs_imp, on the RMSE on the training set is, we look at the out-of-bag error (oob). The features tested are garagetype and exterqual, since they showed to be the two features with the highest pair correlation in the training set.

l = dict([(k,[]) for k in ['features','oob_score']])
def get_oob(df,n:str,l=l):
    l['features'].append(n)
    print(l)
    m = RandomForestRegressor(
        n_estimators=30,
        min_samples_leaf=5,
        max_samples=500,
        max_features=0.5,
        n_jobs=-1,
        oob_score=True,
        random_state=seed,
    )
    m.fit(df, y)
    l['oob_score'].append(m.oob_score_)
    print()
    print(f'oob using {n}: {m.oob_score_}')
    print(l)
    return m.oob_score_

The baseline oob score for xs_imp.

get_oob(xs_imp,'xs_imp')

{'features': ['xs_imp'], 'oob_score': []}

oob using xs_imp: 0.843435210902987
{'features': ['xs_imp'], 'oob_score': [0.843435210902987]}

0.843435210902987

The oob score for xs_imp is slightly lower than the one for xs. Considering, that there are 83 columns in xs and 21 in xs_imp, the slight decrease in the oob score shows that most of the difference in features between the two is made up of columns that don’t decrease the RMSE of the model on the training data.

get_oob(xs,'xs')

{'features': ['xs_imp', 'xs'], 'oob_score': [0.843435210902987]}

oob using xs: 0.8521572851913823
{'features': ['xs_imp', 'xs'], 'oob_score': [0.843435210902987, 0.8521572851913823]}

0.8521572851913823

The two columns garagetype and exterqual are dropped and the oob score is computed using the remaining features in xs_imp. One notices that the oob_score is lower for the case where only one of the two features is dropped and higher if both are dropped together. Accounting for this, both features are dropped together.

Drop One Feature At A Time

Drop garagetype and exterqual one at a time, with replacement.

{
    c: get_oob(xs_imp.drop(c, axis=1),f'xs_imp.drop-{c}')
    for c in (
        "garagetype",
        "exterqual",
    )
}

{'features': ['xs_imp', 'xs', 'xs_imp.drop-garagetype'], 'oob_score': [0.843435210902987, 0.8521572851913823]}

oob using xs_imp.drop-garagetype: 0.8447838576955676
{'features': ['xs_imp', 'xs', 'xs_imp.drop-garagetype'], 'oob_score': [0.843435210902987, 0.8521572851913823, 0.8447838576955676]}
{'features': ['xs_imp', 'xs', 'xs_imp.drop-garagetype', 'xs_imp.drop-exterqual'], 'oob_score': [0.843435210902987, 0.8521572851913823, 0.8447838576955676]}

oob using xs_imp.drop-exterqual: 0.8443621750779751
{'features': ['xs_imp', 'xs', 'xs_imp.drop-garagetype', 'xs_imp.drop-exterqual'], 'oob_score': [0.843435210902987, 0.8521572851913823, 0.8447838576955676, 0.8443621750779751]}

{'garagetype': 0.8447838576955676, 'exterqual': 0.8443621750779751}

Drop Both Features Together

Drop both features together and compute the oob_score

to_drop = [
    "garagetype",
    "exterqual",
]
get_oob(xs_imp.drop(to_drop, axis=1),f'xs_imp.drop-{to_drop}')

{'features': ['xs_imp', 'xs', 'xs_imp.drop-garagetype', 'xs_imp.drop-exterqual', "xs_imp.drop-['garagetype', 'exterqual']"], 'oob_score': [0.843435210902987, 0.8521572851913823, 0.8447838576955676, 0.8443621750779751]}

oob using xs_imp.drop-['garagetype', 'exterqual']: 0.8500505935232953
{'features': ['xs_imp', 'xs', 'xs_imp.drop-garagetype', 'xs_imp.drop-exterqual', "xs_imp.drop-['garagetype', 'exterqual']"], 'oob_score': [0.843435210902987, 0.8521572851913823, 0.8447838576955676, 0.8443621750779751, 0.8500505935232953]}

0.8500505935232953

Evaluate oob_scores

Create a DataFrame and sort values by oob_score in descending order.

df_oob = pd.DataFrame(l).sort_values(by='oob_score',ascending=False)
df_oob

	features	oob_score
1	xs	0.852157
4	xs_imp.drop-['garagetype', 'exterqual']	0.850051
2	xs_imp.drop-garagetype	0.844784
3	xs_imp.drop-exterqual	0.844362
0	xs_imp	0.843435

New Train & Validation Sets Using Resulting Feature Set

The resulting Datasets have the two features removed. These two datasets are the new baseline datasets that all the following models are fitted/evaluated on.

xs_final = xs_imp.drop(to_drop, axis=1)
valid_xs_final = valid_xs_imp.drop(to_drop, axis=1)

Exporting and immediately importing the datasets in their current state as .pkl files using the fastai proprietary functions save_pickle and load_pickle respectively.

save_pickle("xs_final.pkl", xs_final)
save_pickle("valid_xs_final.pkl", valid_xs_final)

xs_final = load_pickle("xs_final.pkl")
valid_xs_final = load_pickle("valid_xs_final.pkl")

Baseline RMSE Scores

m = rf(xs_final, y)
m_rmse(m, xs_final, y), m_rmse(m, valid_xs_final, valid_y)

(0.129697, 0.140712)

dfi = rf_feat_importance(m, xs_final)
plot_fi(dfi) 

<AxesSubplot: title={'center': 'Feature Importance Plot'}, xlabel='Feature Importance Score', ylabel='Feature'>

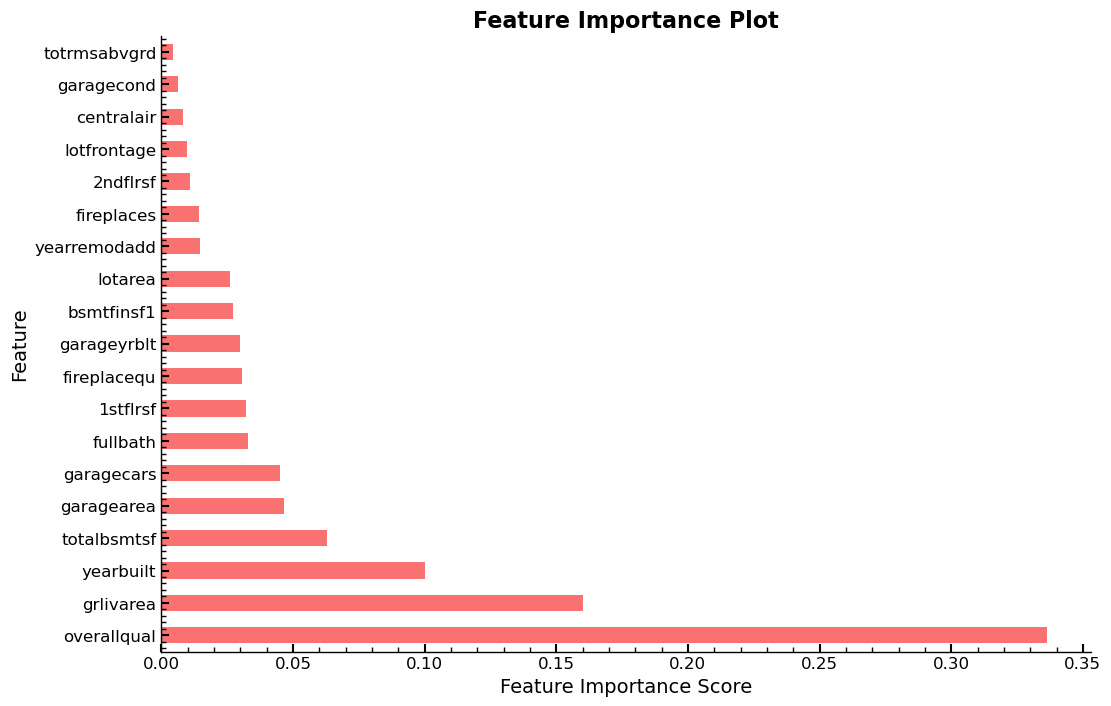
Exploring The Impact of Individual Columns

Column overallqual has shown to be the most important column overall relative to all the other columns in the dataset. This gives reason, to get a detailed look at its unique value distribution. The feature has ten levels, ranging from two to ten in ascending order. It describes the “overall quality” of an object and judging by the feature importance plots, it is the strongest predictor for variable saleprice.

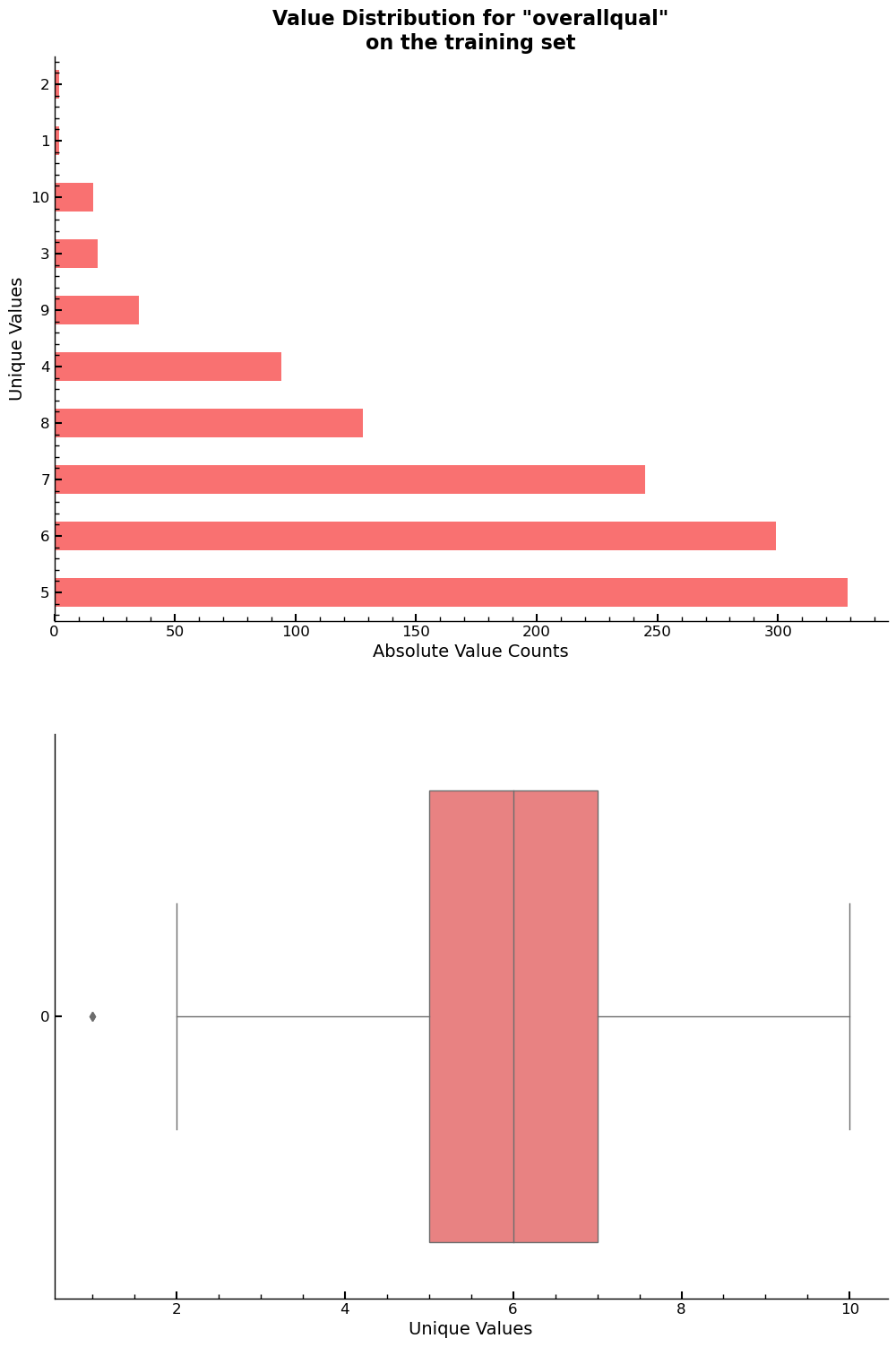
The value counts and the box plot for overallqual are given below.

xs_final["overallqual"].value_counts().reset_index().sort_values(by='index',ascending=False)

	index	overallqual
7	10	16
5	9	35
3	8	128
...	...	...
6	3	18
9	2	2
8	1	2

10 rows × 2 columns

fig, ax = plt.subplots(2,1,figsize=(8,10))
ax= plt.subplot(211)
xs_final["overallqual"].value_counts().plot.barh(ax=ax)
ax.set_xlabel("Absolute Value Counts")
ax.set_ylabel("Unique Values")
ax.set_title(f'Value Distribution for "overallqual"\non the training set')
ax = plt.subplot(212)
sns.boxplot(xs_final["overallqual"],orient='h',ax=ax)
ax.set_xlabel("Unique Values")
plt.show()

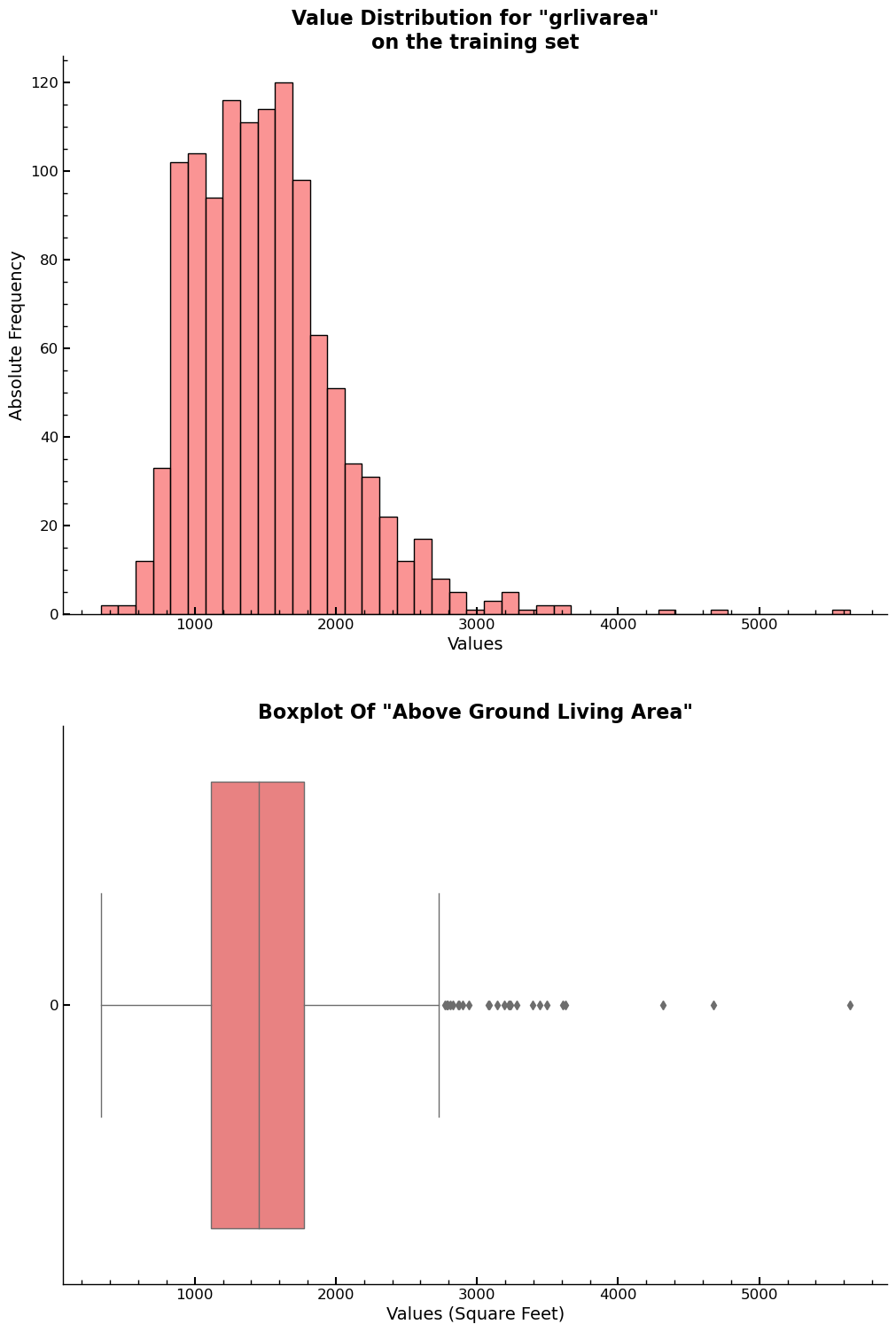
Another important feature is grlivarea, which gives the area above ground in square feet.

fig, ax = plt.subplots(2,1,figsize=(10,10))
ax=plt.subplot(211)
sns.histplot(x=xs_final["grlivarea"],ax=ax)
ax.set_xlabel("Values")
ax.set_ylabel("Absolute Frequency")
ax.set_title('Value Distribution for "grlivarea"\non the training set')
ax = plt.subplot(212)
sns.boxplot(xs_final["grlivarea"],orient='h',ax=ax)
plt.title('Boxplot Of "Above Ground Living Area"')
plt.xlabel("Values (Square Feet)")
plt.show()

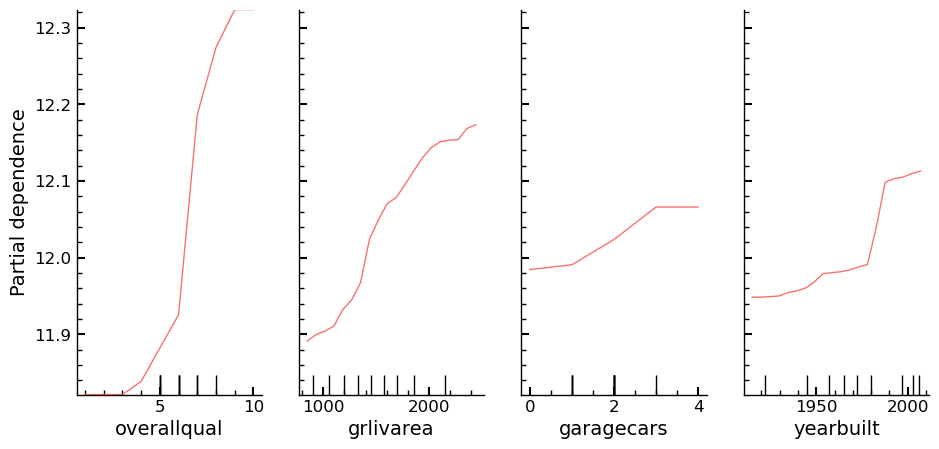
While the univariate distributions of the features are of interest, they don’t show the relationship between independent and dependent variable. The relationships can be visualized using a Partial Dependence plot.

Partial Dependence

Plots of partial dependence for the most important columns in the slimmed down dataset. The plot is part of the scikit-learn library and its documentation can be found here: partial_dependence Documentation. The plot is like an individual conditional expectation plot, which lets one calculate the dependence between the dependent variable and any subset of the independent variables. Four columns that have shown several times that they are of high importance for the predictions of the dependent variable are chosen and their partial dependence plots are created.

The output shows that overallqual and yearbuilt show a high correlation with the dependent variable. Not only that though, the plot also shows how the assumed change in the value of the dependent variable, \(\frac{\partial \mathrm{saleprice}}{\partial x_{i}}\,\,\mathrm{for}\,\,\mathrm{i}\, \in \{\mathrm{overallqual},\, \mathrm{grlivarea},\, \mathrm{garagecars},\, \mathrm{yearbuilt}\}\)

ax = plot_partial_dependence(
    m,
    xs_final,
    ["overallqual", "grlivarea", "garagecars", "yearbuilt"],
    grid_resolution=20,
    n_jobs=-1,
    random_state=seed,
    n_cols=4,
)

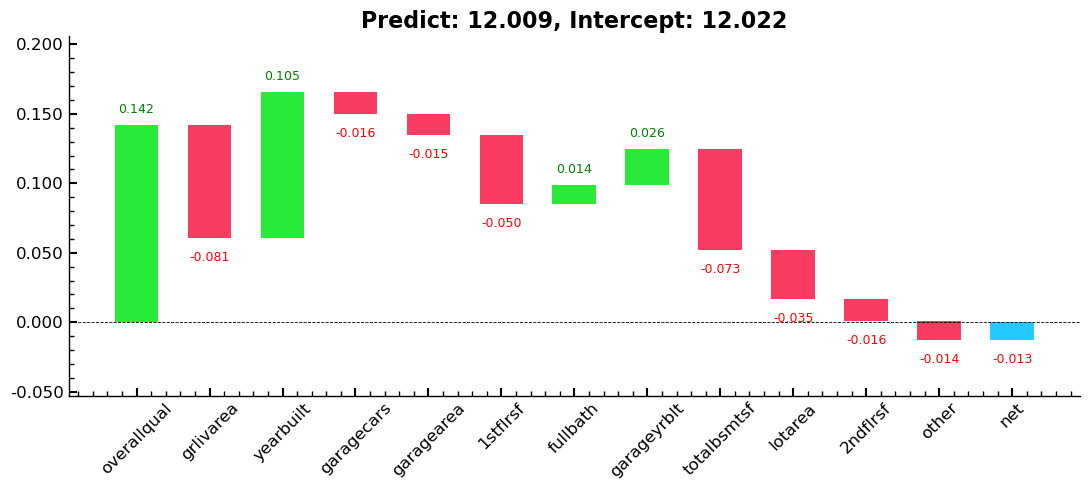
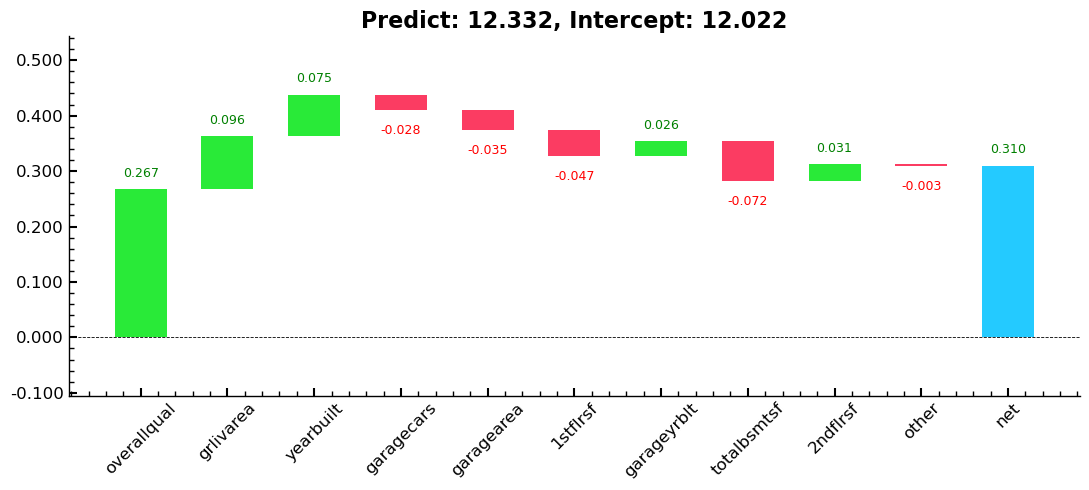
Tree Interpreter

A plot using treeinterpreter from treeinterpreter, and we try to answer the question:

For predicting with a particular row of data, what were the most important factors, and how did they influence that prediction?

row = valid_xs_final.sample(n=2, random_state=seed)
predict, bias, contributions = treeinterpreter.predict(m, row.values)
# rounding for display purposes
predict = np.round(predict,3)
bias = np.round(bias,3)
contributions = np.round(contributions,3)

print(
    f'For the first row in the sample predict is: {predict[0]},\n\nThe overall log average of column "saleprice": {bias[0]},\n\nThe contributions of the columns are:\n\n{contributions[0]}'
)

For the first row in the sample predict is: [12.009],

The overall log average of column "saleprice": 12.022,

The contributions of the columns are:

[ 0.142 -0.081  0.105 -0.016 -0.015 -0.05   0.014  0.026 -0.073 -0.005
 -0.007 -0.035  0.002  0.009  0.    -0.009 -0.001 -0.016 -0.003]

for e in zip(predict, bias, contributions):
    waterfall(
        valid_xs_final.columns,
        e[2],
        Title=f"Predict: {e[0][0]}, Intercept: {e[1]}",
        threshold=0.08,
        rotation_value=45,
        formatting="{:,.3f}",
    )
plt.show()

Example of how to use the treeinterpreter on a single sample.

Example of how to use the treeinterpreter on a single sample.

Entire Series: